深度学习 - TORCH
1. Backward梯度计算
1.1. 举例一
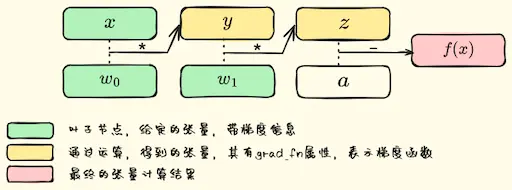
1.1.1. 神经网络构建
1.1.2. 反向传播
求导链式法则
1.1.3. 代码
import torch
import numpy as npx = torch.from_numpy(2 * np.ones((2, 2), dtype=np.float32))
x.requires_grad_(True)
w0 = torch.from_numpy( 5*np.ones((2, 2), dtype=np.float32) )
w0.requires_grad_(True)
w1 = torch.from_numpy( 5*np.ones((2, 2), dtype=np.float32) )
w1.requires_grad_(True)
a = torch.from_numpy( 10*np.ones((2,2), dtype=np.float32) )
y = w0 * x
z = w1 * y
f = a - z
print(y)
f.backward(torch.ones_like(x))
print(x.grad)输出
tensor([[10., 10.],
[10., 10.]], grad_fn=<MulBackward0>)
tensor([[-25., -25.],
[-25., -25.]])1.requires_grad: True表示该Tensor可计算梯度,直接在创建tensor时指定属性requires_grad=True,或使用函数x.requires_grad_(True)
2.grad_fn: 通过运算得到的Tensor(非自己创建的tensor),会自动被赋值grad_fn属性。该属性表示梯度函数
3.gradient: 表示输出tensor对当前调用backward函数的Tensor的导数,
1.2. 举例二
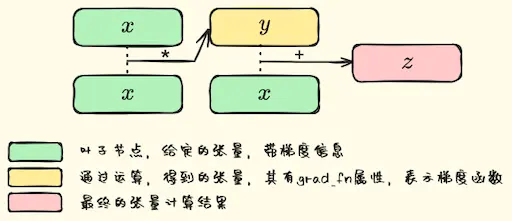
1.2.1. 神经网络构建
1.2.2. 参考代码
x = torch.tensor([1.,2.,3.], requires_grad=True)
y = x**2
z = y+x
z.backward()
print(x.grad)
print(y.grad)1.2.3. 整理点
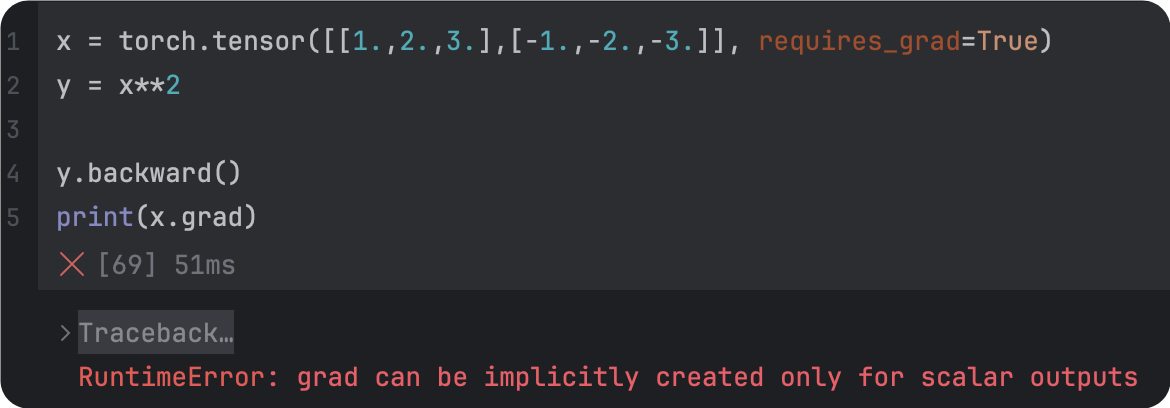 | 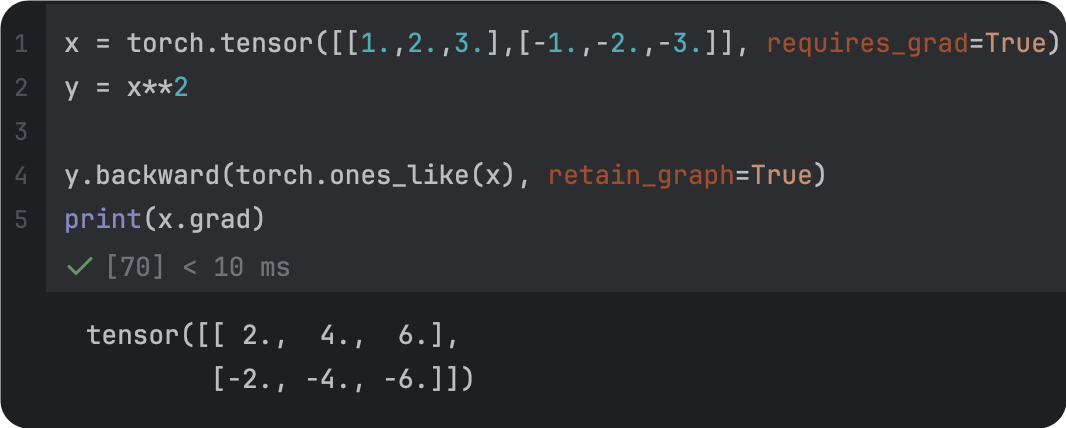 |
|---|---|
backward的维度一致 | 改正后 |
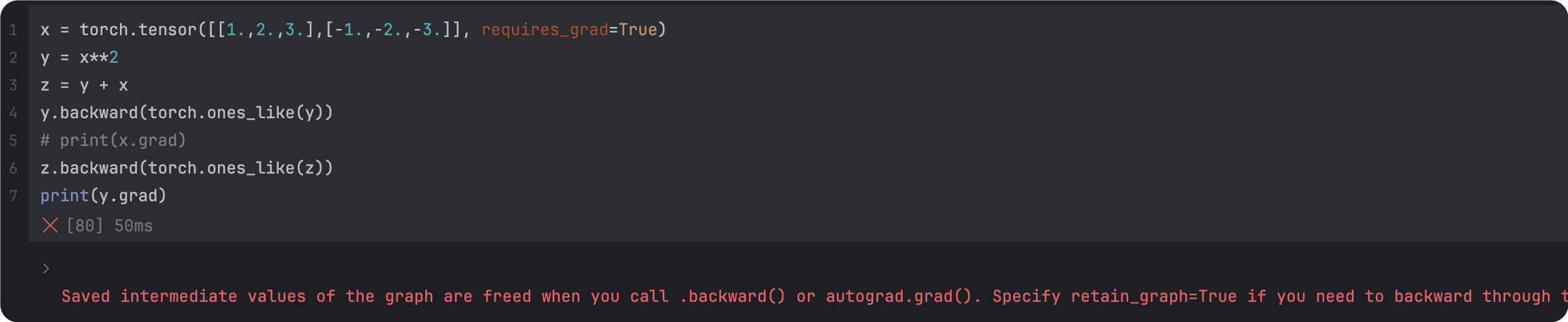 | 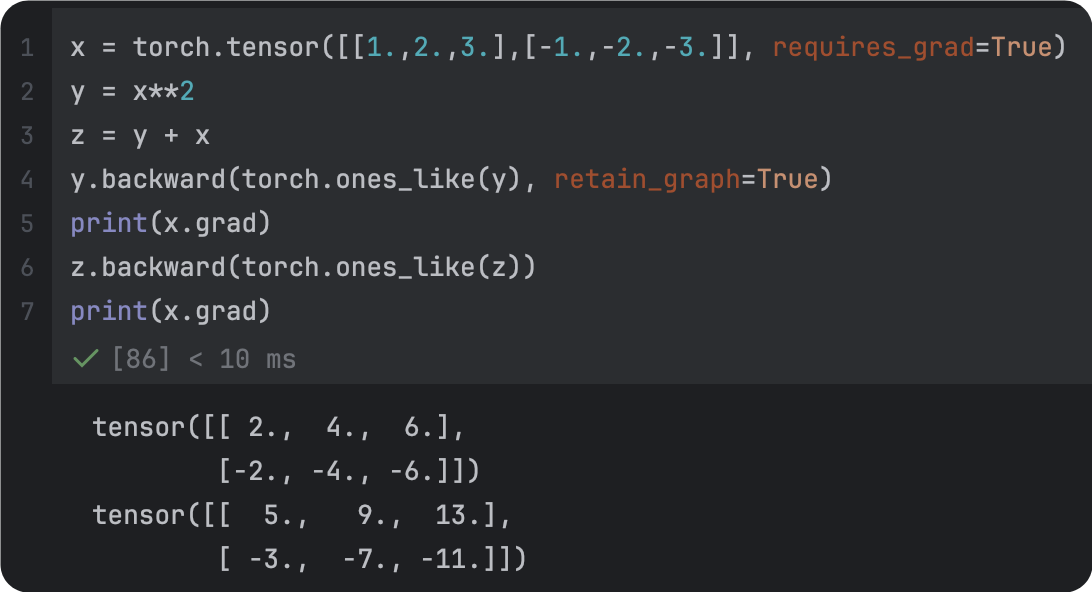 |
|---|---|
| 改正后 |
 | 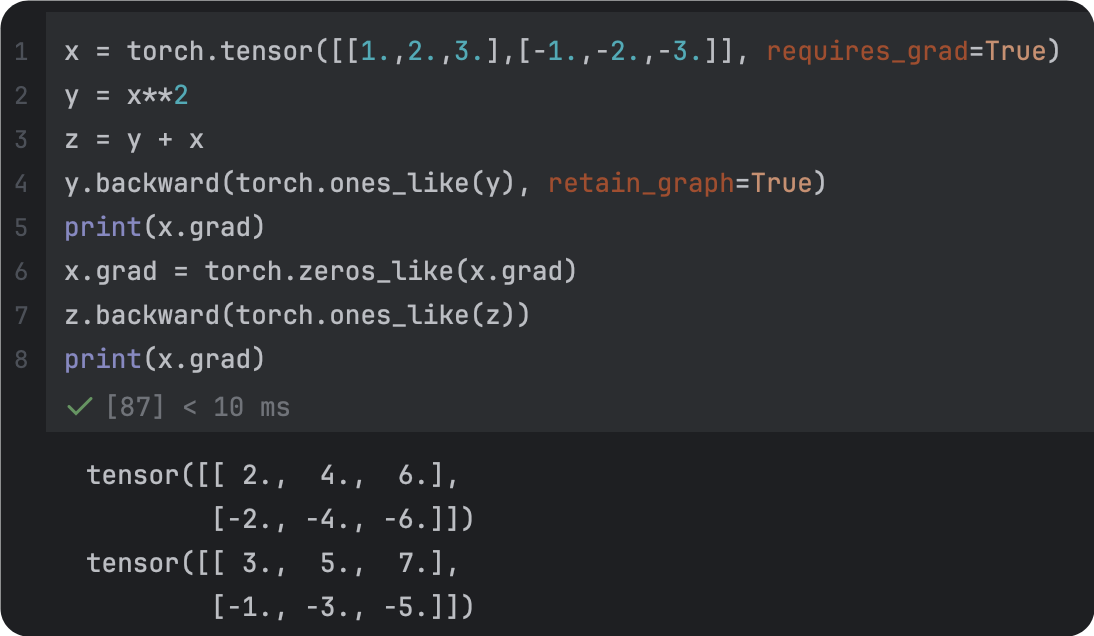 |
|---|---|
| 未清理 | 改正后 |
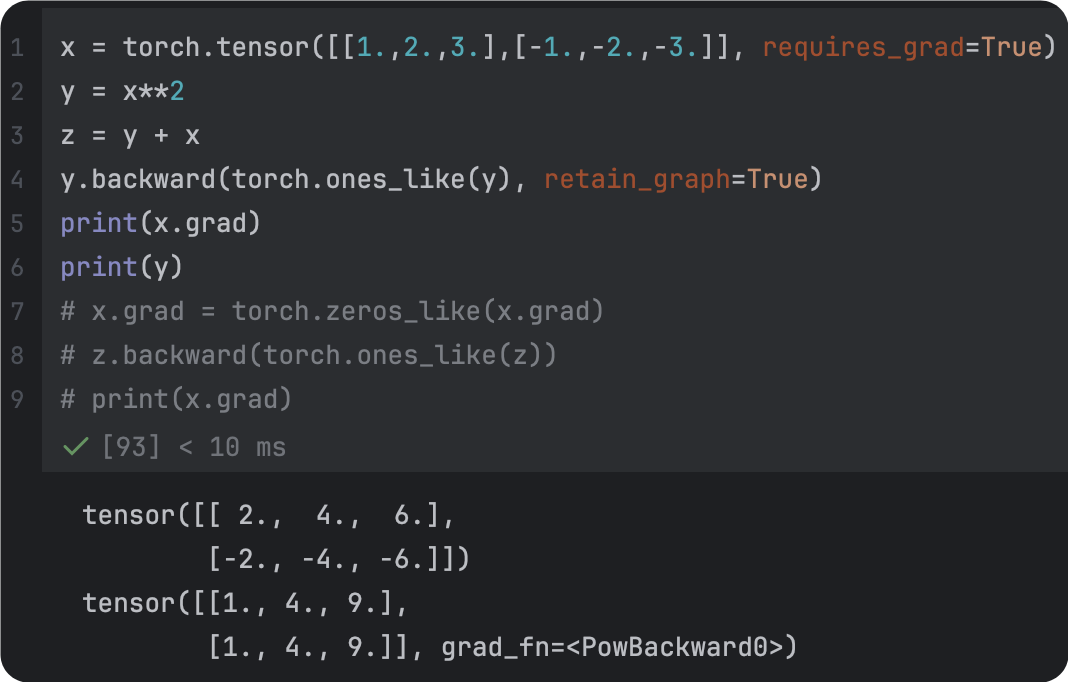 | 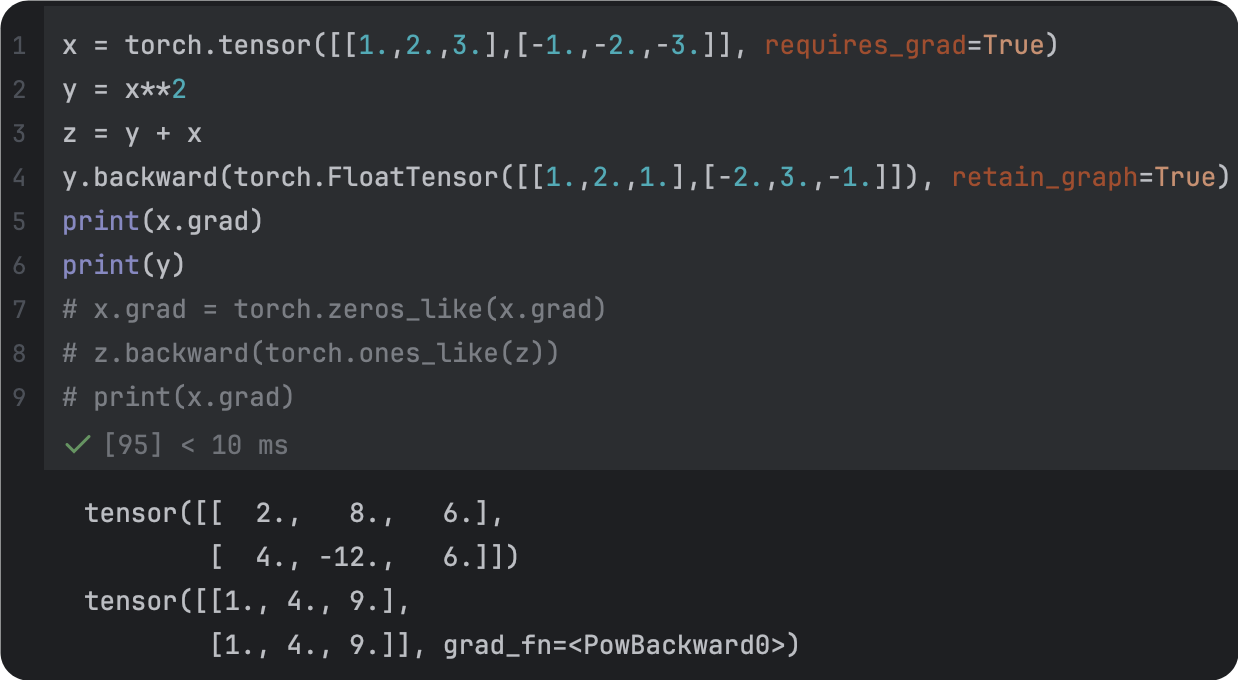 |
|---|---|
| 梯度参数全为1 | 梯度参数指定为维度一致的张量 |
1.retain_gragh: Pytorch的计算图是动态的,每完成一次迭代(每一次backward后),计算图就会被丢弃,所以,在backward以后,backward。为了backward以后,计算图不被丢弃,要把retain_gragh设定为True
参考
1.Backward函数
2.Backward解释
3.计算图